For some years now, NASA has been using what are called thermoelectric materials to power its space probes. The probes travel such great distances from our sun that solar panels are no longer an efficient source of power. So NASA imbeds a nuclear material in a radioisotope thermal generator, where it decays, producing heat energy. That energy is then converted by thermoelectric materials into the electricity that powers the space probe. The same technology is now being explored for more earthly applications, for example, to capture heat lost in the exhaust of automobiles to produce electricity for the vehicle.
Thermoelectric materials are a hot new technology that is now being studied intensively by researchers funded by the U.S. Department of Energy's Energy Frontier Research Centers. Oliver Delaire, a Shull fellow at ORNL, is part of such a collaboration, this one led by an EFRC at the Massachusetts Institute of Technology. Delaire uses neutron scattering and computer simulation to investigate the microscopic structure and dynamics of thermoelectric materials so that researchers can make them more efficient for new, energy-saving applications.
Thermoelectrics are adaptable for both heating and for cooling applications. These materials can convert low-grade heat that is wasted in an industrial process, or in the exhaust system of a vehicle, into electricity. Or they can transport heat from an external source of power and manipulate it to cool a surface.
But there are limitations in the materials themselves. "Right now the materials may be on the order of 10 percent efficiency," Delaire said. "If we can make them two or three times better, if we can get 30% efficiency, that would get people very excited, and it would be much more viable economically."
The researchers want to improve their understanding of phonons, the atomic vibrations that transport heat through thermoelectric materials. "Neutron scattering is unmatched in its ability to probe the atomic vibrations in the crystals," Delaire said. "This is one of the fundamental blocks in the process that we need to understand better."
At ORNL, Delaire and his collaborators are using the Time of Flight spectrometers at SNS—ARCS and CNCS—and the HB-3 Triple-Axis Spectrometer at the High Flux Isotope Reactor (HFIR).
"The SNS instruments offer more power," Delaire said. "They can sample the whole parameter space very efficiently. They offer a unique opportunity in a single experiment to sample all the types of atomic vibrations, all the phonons inside the solid. And once we have this information, we can reconstruct the microscopic thermoconductivity, which is really the property we are trying to understand."
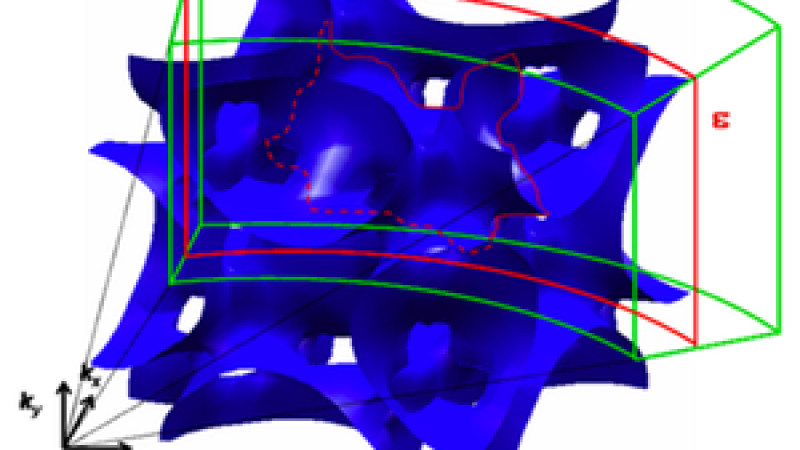
The single crystals are grown at ORNL. There are two high-temperature materials, PbTe (lead telluride) and La3Te4 (lanthanum telluride) for heat recovery and FeSi (iron silicide) for refrigeration applications. Single crystals offer advantages in neutron science. They can be measured on the TOF instruments at a series of orientations, each orientation giving a comprehensive data set. Combining these sets gives the researchers a complete picture, much like tomography.
"By doing this experiment using the high neutron flux here at SNS we are able to really map out the space, and that is really where the big advance is," Delaire said. "Previously we were only able to look at a few points in the space, and that is like looking with a flashlight. With the flux we have at SNS, we turn on the overhead lights and see the whole room all at once."
Once they have a view of the volume of data, the researchers then use the triple-axis spectrometer at HFIR to zero in and look at pinpoints of phonon vibrations in that region. Next, ab initio computational methods simulate the data that the instruments have generated. These simulations are based on quantum mechanics, which gives the researchers a direct comparison between the neutron science measurements and fundamental theory and theoretical predictions.
In 2010, the researchers uncovered an important coupling between thermal disorder and the electronic structure of FeSi. This type of coupling between thermal disorder and electronic structure at finite temperature could prove to be important in many materials, including thermoelectrics. The research is funded by an Energy Frontier Research Center at MIT and involves a dozen investigators, including Delaire and David Singh, a solid-state theorist in materials science at ORNL. Samples are also contributed by researchers at Boston College. Delaire, Singh and some of the MIT researchers are involved in the computation.
This research was funded by the U.S. Department of Energy (DOE) Office of Basic Energy Sciences.
Published Work
O. Delaire , K. Marty , M. B. Stone , P. R. C. Kent , M. S. Lucas , D. L. Abernathy , D. Mandrus , B. C. Sales. "Phonon softening and metallization of a narrow-gap semiconductor by thermal disorder," Proceedings of the National Academy of Sciences of the United States of America. PNAS 108(12), 4725-4730 (Mar. 22, 2011).
Brian C. Sales, Olivier Delaire, Michael A. McGuire, and Andrew F. May, "Thermoelectric properties of FeSi and Related Alloys: Evidence for Strong Electron-Phonon Coupling," PACS: 72.20.Pa, 63.20.Kd. Accepted in Phys. Rev. B.